At the AEI 10m Prototype, we are currently building up the Sub-SQL Interferometer, which is designed to be limited by the standard quantum limit (SQL) in order to test techniques to surpass it.

What is quantum noise?

The advent of quantum mechanics, the concept that physics at the sub-microscopic level obeyed statistical mechanics and were subject to uncertainty, revolutionised physics in the 20th century. This statistical nature and uncertainty consequently results in noise in any system. In everyday life, this noise is negligibly small especially in comparison with technical and classical noise, e.g. the flickering of light from a lamp due to quantum mechanics are inconceivably small compared to the flickering due to the technical noise of the electricity supply. Gravitational wave detectors however have been designed to be extremely sensitive instruments where all other classical and technical noise sources have been suppressed via advanced techniques and technologies such that quantum noise is no longer hidden beneath them. Quantum noise affects gravitational wave detectors via two different mechanisms: quantum shot noise and quantum radiation pressure noise.

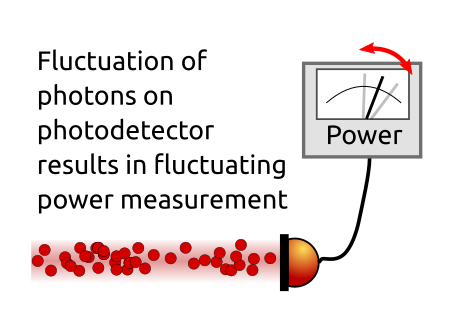
Shot noise is measured directly at the photodetector. In the photon picture (in contrast to the wave description of light), photons will not arrive at the photodetector as a ‘steady stream’ of particles but rather as single events with some quantum mechanical statistics. This variation in number of photons hitting the photodetector and the timing of the photons is equivalent to amplitude and phase noise of the light.

Radiation pressure is the phenomenon that despite being massless, light can transfer momentum to objects (opto-mechanical coupling). Gravitational wave detectors employ suspensions to isolate the test mass mirrors from ground motion, and hence they behave as free masses (at least above their resonance frequencies). The quantum nature of the light in the interferometer means there is a noisy ‘quantum force’ pushing on the test mass mirrors, changing their positions and showing up in the output signal of the interferometer.

How does quantum noise lead to the Standard Quantum Limit?

The effect of shot noise in an interferometer can indeed be suppressed by increasing the optical power in the interferometer. Although shot noise actually increases with more power proportionally to the square root of the optical power, the response of the interferometer (the strength of the output signal) increases linearly. The overall signal-to-noise ratio is therefore proportional to the square root of optical power. Note that shot noise is a frequency independent noise; however, the response of gravitational wave detectors starts to decrease at high frequency and hence the overall effect of shot noise in the frequency domain is a flat noise at low frequency.

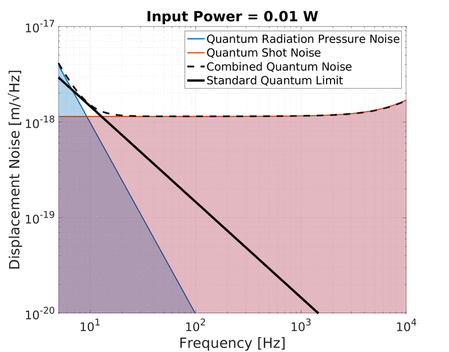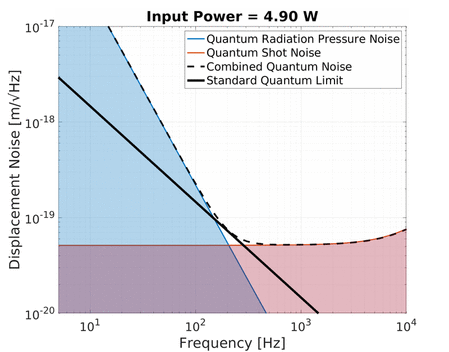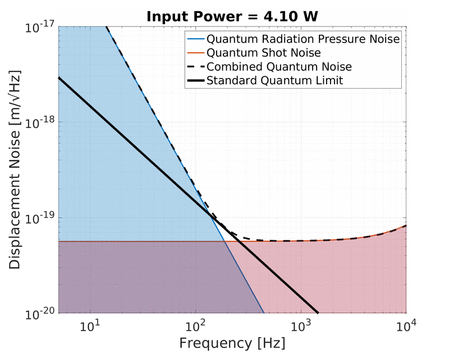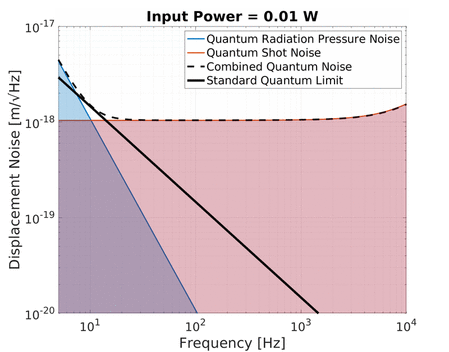
Quantum radiation pressure noise on the other hand is strongly frequency dependent. The displacement of a free mass subject to a sinusoidal force decreases with frequency squared. As a result the noise due to quantum radiation pressure at low frequencies can be larger than shot noise if the optical power is high enough. Increasing the optical power in the interferometer pushes up this 1/f² noise curve up with a square root relation.

An increase in power therefore simultaneously increases the quantum radiation pressure noise while decreasing the shot noise of an interferometer. This is shown in the animation below:

Notice the black line traced out by the crossover between quantum radiation pressure noise and shot noise as the optical power is varied. This is the Standard Quantum Limit (SQL), which describes the minimum level of total quantum noise in a certain interferometer at each frequency which can be achieved by only adjusting the optical power. This phenomenon shows what is predicted by the Heisenberg’s uncertainty principle of the displacement and momentum (see below). Keep in mind that the quantum radiation pressure noise is dependent on the mass of the test mass mirrors since a larger mass would be displaced less due to radiation pressure and hence have a lower SQL. This is why full scale gravitational wave detectors aim to use as large masses as possible (e.g. Advanced LIGO and Advanced Virgo use 40 kg mirrors, and KAGRA uses 23 kg). In contrast, we at the AEI 10 m Prototype aim to investigate the SQL and overcoming it and hence we use relatively light mirrors (0.1 kg) to enhance the SQL rather than suppress it.

How is the SQL derived from displacement and momentum?

A more mathematically rigid method of describing the SQL can be made by considering the displacement and momentum of the mirrors. Quantum mechanics tells us that displacement, \(x\), and momentum, \(p\), are operators that do not commute (i.e. they are correlated):

\( \left[ x(t), p(t) \right ] \approx i \hbar \)

This results in the Heisenberg’s uncertainty principle:

\( | \Delta x(t) | \cdot | \Delta p(t) | \geq i \hbar \)

Let us assume the test mass is free (suspension is ignored). The momentum at time, \(t\), influences the displacement at a later time, namely

\( \Delta x(t+ \tau) = \Delta x(t) + \Delta p(t) \tau / m \)

This means that the displacements at different time do not commute. The minimum value of the fluctuation is then given by

\( \Delta x(t) \geq \sqrt{\hbar \tau / 2 m} \)

Here the measurement time is given as

\( \tau \approx 1/\pi f\)

and the power spectral density is given by

\( S_{x} = |\Delta x |^{2} \tau \)

Therefore, we have

\( S_{x} \geq S_{SQL} = 2 \hbar / m\Omega^{2} \)

This is the SQL. In a Michelson interferometer with Fabry-Perot arm cavities, we use \(m/4\) instead of \(m\) as our target motion is the differential-mode motion of 4 mirrors. We also divide this by \(L^2\) (\(L\) is the arm length) and take the square root of it when we show the sensitivity in strain.

How can we exceed the limit?

It is because we are actually measuring the force with a gravitational-wave detector. Those \(x\) and \(p\) shown above are the initial location and the initial momentum, respectively. If we want to measure the initial \(x\) and \(p\), quantum mechanics does not allow us to increase the accuracy for both \(x\) and \(p\); we cannot exceed the SQL. However, the initial information has already disappeared in the gravitational-wave detector. Environmental decoherence has hidden the quantum property, which we actually do not need to measure the gravitational waves.

Nevertheless, the SQL exists in the gravitational-wave detector if we aim at the conventional measurement of the phase quadrature component. Unlike the operator \(x\), the output field operator commutes at different times. But there are two components in the phase quadrature that do not commute, which results in the limit. Each of them is a quadrature component of the vacuum fluctuation coming in from the dark port of the interferometer. One is the source of shot noise and the other is the source of radiation pressure noise. Since the latter appears as a result of the opto-mechanical coupling, the SQL reads the same value as the one derived above. This, however, does not impose a fundamental limit, and hence there can be various ways to overcome the SQL in the sensitivity curve of the gravitational-wave detector.

If we aim at the measurement of the initial \(x\) and \(p\), or those quantities recovered by the measurement (conditional \(x\) and \(p\)), the SQL will be the limit that cannot be overcome. The measured variance of \(x\) and \(p\), together with their covariance, will follow the Heisenberg’s uncertainty principle. Interestingly, in order to prepare this conditional state, we need an interferometer whose classical noise is lower than the SQL (the beatable SQL). So, the SQL is finally important.

References

S.L. Danilishin, F.Y. Khalili, ‘Quantum Measurement Theory in Gravitational-Wave Detectors’, Living Reviews in Relativity, 15(5), (2012). DOI: https://doi.org/10.12942/lrr-2012-5

S.L. Danilishin, F.Y. Khalili, & H. Miao, ‘Advanced quantum techniques for future gravitational-wave detectors’, Living Reviews in Relativity, 22(2), (2019). DOI: https://doi.org/10.1007/s41114-019-0018-y

S. Hild, A Basic Introduction to Quantum Noise and Quantum-Non-Demolition Techniques. In: Bassan M. (eds) Advanced Interferometers and the Search for Gravitational Waves. Astrophysics and Space Science Library, vol 404. Springer, Cham. (2014) DOI: 10.1007/978-3-319-03792-9_11